Research

My research is motivated by problems arising from medicine and public health, and focuses on developing flexible, scalable, and interpretable statistical methods for modeling continuously monitored health data. Specifically, I’m focusing on two application areas: (1) hemodynamics data collected throughout cardiac surgeries; and (2) physical activity data collected using accelerometers. The scale and complexity of these data demand novel analytic tools and motivate my research.

Hemodynamics Data

Coronary Artery Bypass Grafting (CABG), also known as heart bypass (心脏搭桥), is a surgical procedure that improves blood flow to the heart. With more than 800,000 cases performed worldwide each year, it is the most common cardiac surgery. However, due to its invasive nature, CABG places significant stress on the body and can lead to organ damage. For instance, 20%-40% of CABG patients develop Acute Kidney Injury (AKI) within 48 hours post-surgery.

Can we do better? I am working closely with a team of anesthesiologists from the Johns Hopkins Medical Institute to investigate the relationship between intraoperative hemodynamics and post-surgical organ damage outcomes. We aim to identify optimal hemodynamic management strategies that minimize the risk of organ damage.

Wearable Device Data

Many of us wear devices like Fitbit, Apple Watch, and Dexcom Stelo to continuously track activity levels, sleep, and glucose values throughout the day. These high-resolution data provide an unprecedented level of detail in studying health and hold immense potential for applications ranging from personalized health monitoring to clinical trial innovation. However, alongside these opportunities come significant challenges: the data are typically large, high-dimensional, and complex in structure. My work in this area focuses on developing methods that effectively address these challenges.

Related publication

• Zhou, X., Cui, E., Sartini, J. and Crainiceanu, C.M., 2025. Prediction Inference Using Generalized Functional Mixed Effects Models. arXiv preprint arXiv:2501.07842.
• Sartini, J., Zhou, X., Selvin, L., Zeger, S. and Crainiceanu, C.M., 2024. Fast Bayesian Functional Principal Components Analysis. arXiv preprint arXiv:2412.11340.
• Lu, Y., Zhou, X., Cui, E., Rogers, D., Crainiceanu, C.M., Wrobel, J. and Leroux, A., 2024. Generalized Conditional Functional Principal Component Analysis. arXiv preprint arXiv:2411.10312.
• Zhou, X., Wrobel, J., Crainiceanu, C.M. and Leroux, A., 2023. Analysis of Active/Inactive Patterns in the NHANES Data using Generalized Multilevel Functional Principal Component Analysis. arXiv preprint arXiv:2311.14054.

Prior work

Inference for massive and distributed longitudinal data

Longitudinal data are ubiquitous in medical research and linear mixed models (LMMs) are powerful tools for analyzing them. Statistical inference of variance component parameters has traditionally relied on bootstrap, which becomes prohibitively slow on large datasets.

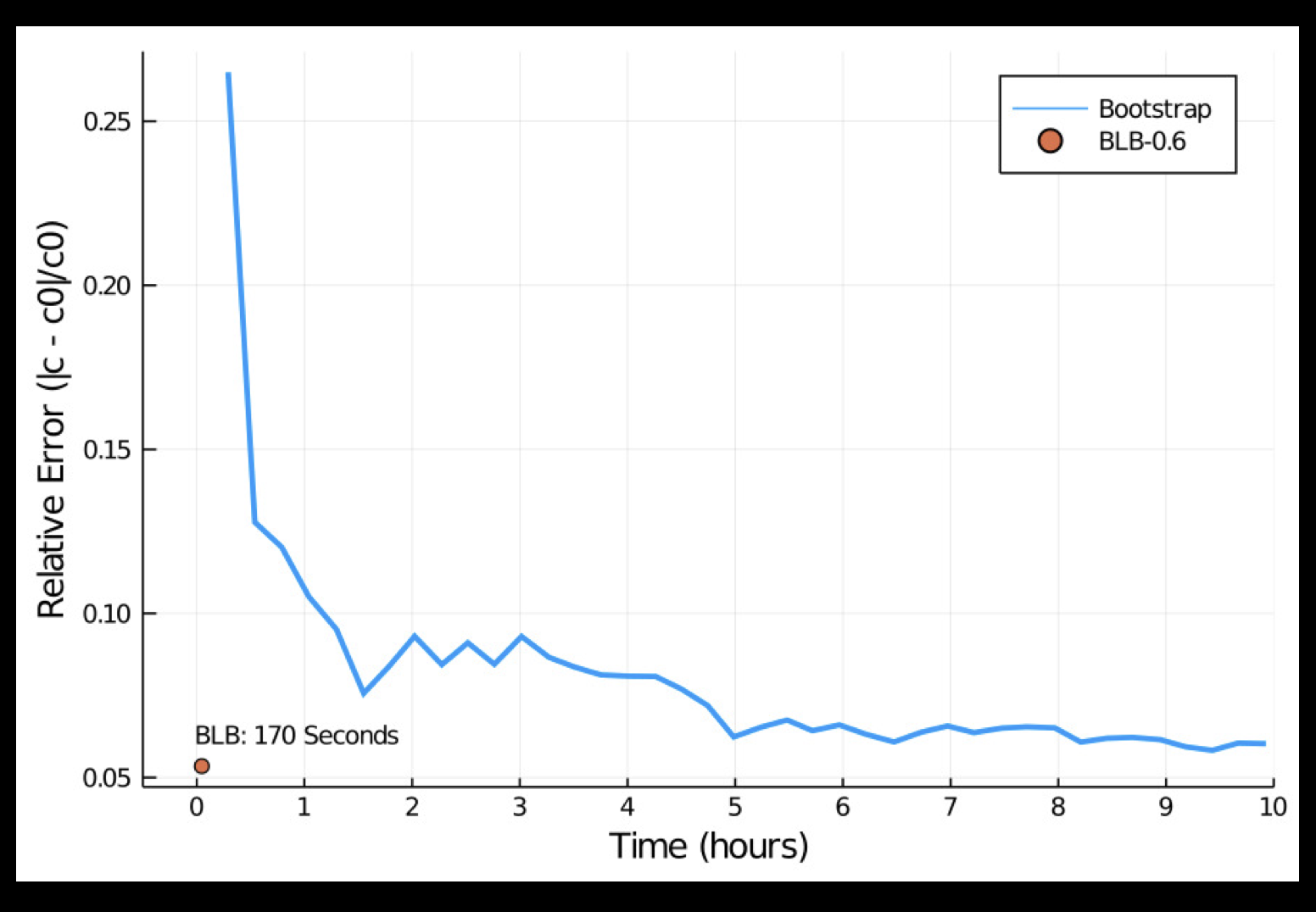
My work in this area has led to the Bag of Little Bootstrap method for massive longitudinal data, which reduces the computational cost from \(O(BNq^3)\) to \(O(Bbq^3)\), where \(B\) is the number of bootstrap replicates, \(N\) is the number of subjects, \(q\) is the number of random effect parameters, and \(b \ll N\). It achieves 200 times speedup on the scale of 1 million subjects (20 million total observations), and is the only currently available tool that can handle more than 10 million subjects (200 million total observations) on a laptop.

Related publication

• Zhou, X., Zhou, J.J. and Zhou, H., 2022. Bag of little bootstraps for massive and distributed longitudinal data. Statistical Analysis and Data Mining: The ASA Data Science Journal, 15(3), pp.314-321.

Software

• MixedModelsBLB.jl: A Julia package for analyzing massive longitudinal data using Linear Mixed Models (LMMs) through the Bag of Little Bootstrap (BLB) method.
  • Supports a variety of data interfaces including directly interfacing with databases.
  • Supports parallel processing.
  • Supports both gradient-based and gradient-free solvers.

Inference for constrained and regularized estimation problems

Many statistical learning tasks including Lasso, constrained Lasso, graphical Lasso, matrix completion, and sparse low rank matrix regression can be posed as regularized and/or constrained maximum likelihood estimation that require solving optimization problems of the form

where \(\boldsymbol{\theta}\) denotes model parameters, \(\ell(\boldsymbol{\theta})\) denotes the log-likelihood and quantifies the lack-of-fit between the model and the data, \(P(\boldsymbol{\theta})\) is a regularization function that imposes structure on parameter estimates, and \(\rho\) is a nonnegative regularization strength parameter that trades off the model fit encoded in \(\ell(\boldsymbol{\theta})\) with the desired structure encoded in \(P(\boldsymbol{\theta})\). For many problems of this form, statistical inference for \(\theta\) either did not exist or require substantial problem-specific analysis such as developing new priors or deriving analytic results. For example, extending post-selection inference results for Lasso to the setting where additional constraints are incorporated (constrained Lasso) is not trivial.

My work in this area aims to make statistical inference for such problems much easier. It addresses these challenges by integrating ideas from optimization literature, such as Moreau-Yosida envelopes and proximal maps, with the powerful Bayesian inference machinery. This approach has led to ProxMCMC, a flexible, general, and fully Bayesian inference framework for constrained and regularized estimation.

Related publication

• Zhou, X., Heng, Q., Chi, E.C. and Zhou, H., 2024. Proximal MCMC for Bayesian Inference of Constrained and Regularized Estimation. The American Statistician, pp.1-12.

Software

• ProxMCMCExamples: A repository of Julia code that implements ProxMCMC for Lasso, constrained Lasso, graphical Lasso, matrix completion, and sparse low rank matrix regression.