2024

1. arXiv

   

   Prediction Inference Using Generalized Functional Mixed Effects Models

   Xinkai Zhou, Ejia Cui, Joseph Sartini, and Ciprian Crainiceanu

   arXiv preprint arXiv:2501.07842, 2024

   Abs arXiv Bib

   We introduce inferential methods for prediction based on functional random effects in generalized functional mixed effects models. This is similar to the inference for random effects in generalized linear mixed effects models (GLMMs), but for functional instead of scalar outcomes. The method combines: (1) local GLMMs to extract initial estimators of the functional random components on the linear predictor scale; (2) structural functional principal components analysis (SFPCA) for dimension reduction; and (3) global Bayesian multilevel model conditional on the eigenfunctions for inference on the functional random effects. Extensive simulations demonstrate excellent coverage properties of credible intervals for the functional random effects in a variety of scenarios and for different data sizes. To our knowledge, this is the first time such simulations are conducted and reported, likely because prediction inference was not viewed as a priority and existing methods are too slow to calculate coverage. Methods are implemented in a reproducible R package and demonstrated using the NHANES 2011-2014 accelerometry data.

   @article{zhou2025frim,
     title = {Prediction Inference Using Generalized Functional Mixed Effects Models},
     author = {Zhou, Xinkai and Cui, Ejia and Sartini, Joseph and Crainiceanu, Ciprian},
     year = {2024},
     journal = {arXiv preprint arXiv:2501.07842},
   }

2. arXiv

   

   Fast Bayesian Functional Principal Components Analysis

   Joseph Sartini, Xinkai Zhou, Liz Selvin, Scott Zeger, and Ciprian Crainiceanu

   arXiv preprint arXiv:2412.11340, 2024

   Abs arXiv Bib Code

   Functional Principal Components Analysis (FPCA) is one of the most successful and widely used analytic tools for exploration and dimension reduction of functional data. Standard implementations of FPCA estimate the principal components from the data but ignore their sampling variability in subsequent inferences. To address this problem, we propose the Fast Bayesian Functional Principal Components Analysis (Fast BayesFPCA), that treats principal components as parameters on the Stiefel manifold. To ensure efficiency, stability, and scalability we introduce three innovations: (1) project all eigenfunctions onto an orthonormal spline basis, reducing modeling considerations to a smaller-dimensional Stiefel manifold; (2) induce a uniform prior on the Stiefel manifold of the principal component spline coefficients via the polar representation of a matrix with entries following independent standard Normal priors; and (3) constrain sampling using the assumed FPCA structure to improve stability. We demonstrate the application of Fast BayesFPCA to characterize the variability in mealtime glucose from the Dietary Approaches to Stop Hypertension for Diabetes Continuous Glucose Monitoring (DASH4D CGM) study. All relevant STAN code and simulation routines are available as supplementary material.

   @article{sartini2024fbfpca,
     title = {Fast {B}ayesian Functional Principal Components Analysis},
     author = {Sartini, Joseph and Zhou, Xinkai and Selvin, Liz and Zeger, Scott and Crainiceanu, Ciprian},
     year = {2024},
     journal = {arXiv preprint arXiv:2412.11340},
   }

3. arXiv

   

   Generalized Conditional Functional Principal Component Analysis

   Yu Lu, Xinkai Zhou, Erjia Cui, Dustin Rogers, Ciprian M. Crainiceanu, and 2 more authors

   arXiv preprint arXiv:2411.10312, 2024

   Abs arXiv Bib Code

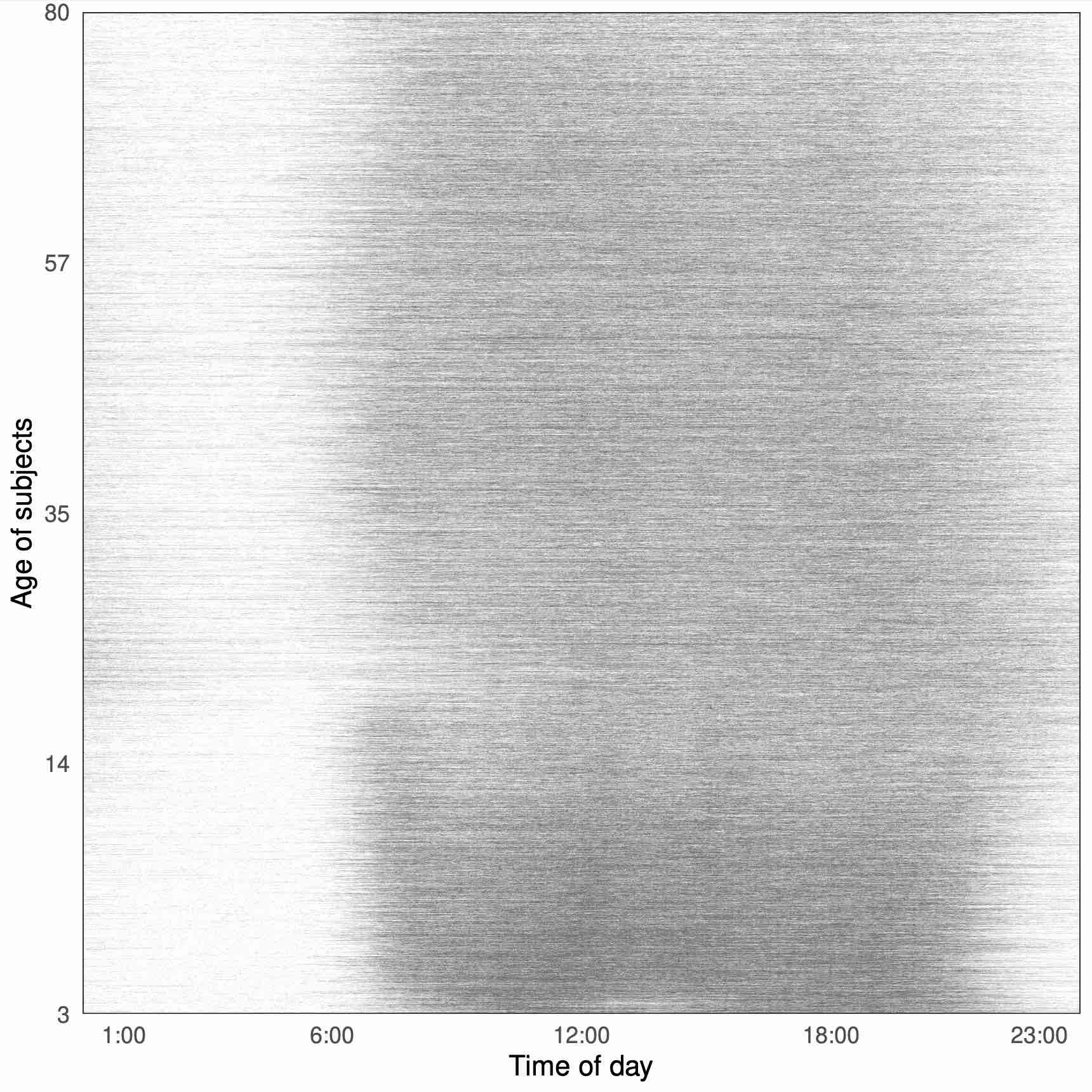
   We propose generalized conditional functional principal components analysis (GC-FPCA) for the joint modeling of the fixed and random effects of non-Gaussian functional outcomes. The method scales up to very large functional data sets by estimating the principal components of the covariance matrix on the linear predictor scale conditional on the fixed effects. This is achieved by combining three modeling innovations: (1) fit local generalized linear mixed models (GLMMs) conditional on covariates in windows along the functional domain; (2) conduct a functional principal component analysis (FPCA) on the person-specific functional effects obtained by assembling the estimated random effects from the local GLMMs; and (3) fit a joint functional mixed effects model conditional on covariates and the estimated principal components from the previous step. GC-FPCA was motivated by modeling the minute-level active/inactive profiles over the day (1,440 0/1 measurements per person) for 8,700 study participants in the National Health and Nutrition Examination Survey (NHANES) 2011-2014. We show that state-of-the-art approaches cannot handle data of this size and complexity, while GC-FPCA can.

   @article{lu2024gcfpca,
     title = {Generalized Conditional Functional Principal Component Analysis},
     author = {Lu, Yu and Zhou, Xinkai and Cui, Erjia and Rogers, Dustin and Crainiceanu, Ciprian M. and Wrobel, Julia and Leroux, Andrew},
     year = {2024},
     journal = {arXiv preprint arXiv:2411.10312},
   }

4. Am. Stat.

   

   Proximal MCMC for Bayesian Inference of Constrained and Regularized Estimation

   Xinkai Zhou, Qiang Heng, Eric C. Chi, and Hua Zhou

   The American Statistician, 2024

   Abs Bib HTML Code

   This article advocates proximal Markov chain Monte Carlo (ProxMCMC) as a flexible and general Bayesian inference framework for constrained or regularized estimation. Originally introduced in the Bayesian imaging literature, ProxMCMC employs the Moreau-Yosida envelope for a smooth approximation of the total-variation regularization term, fixes variance and regularization strength parameters as constants, and uses the Langevin algorithm for the posterior sampling. We extend ProxMCMC to be fully Bayesian by providing data-adaptive estimation of all parameters including the regularization strength parameter. More powerful sampling algorithms such as Hamiltonian Monte Carlo are employed to scale ProxMCMC to high-dimensional problems. Analogous to the proximal algorithms in optimization, ProxMCMC offers a versatile and modularized procedure for conducting statistical inference on constrained and regularized problems. The power of ProxMCMC is illustrated on various statistical estimation and machine learning tasks, the inference of which is traditionally considered difficult from both frequentist and Bayesian perspectives.

   @article{zhou2022proximal,
     author = {Zhou, Xinkai and Heng, Qiang and Chi, Eric C. and Zhou, Hua},
     title = {Proximal MCMC for Bayesian Inference of Constrained and Regularized Estimation},
     journal = {The American Statistician},
     volume = {0},
     number = {0},
     pages = {1--12},
     year = {2024},
     publisher = {Taylor \& Francis},
     doi = {10.1080/00031305.2024.2308821},
   }

2023

1. arXiv

   

   Analysis of Active/Inactive Patterns in the NHANES Data using Generalized Multilevel Functional Principal Component Analysis

   Xinkai Zhou, Julia Wrobel, Ciprian M. Crainiceanu, and Andrew Leroux

   arXiv preprint arXiv:2311.14054, 2023

   Abs arXiv Bib

   Between 2011 and 2014 NHANES collected objectively measured physical activity data using wrist-worn accelerometers for tens of thousands of individuals for up to seven days. Here we analyze the minute-level indicators of being active, which can be viewed as binary (because there is an active indicator at every minute), multilevel (because there are multiple days of data for each study participant), functional (because within-day data can be viewed as a function of time) data. To extract within- and between-participant directions of variation in the data, we introduce Generalized Multilevel Functional Principal Component Analysis (GM-FPCA), an approach based on the dimension reduction of the linear predictor. Scores associated with specific patterns of activity are shown to be strongly associated with time to death. Extensive simulation studies indicate that GM-FPCA provides accurate estimation of model parameters, is computationally stable, and is scalable in the number of study participants, visits, and observations within visits. R code for implementing the method is provided.

   @article{zhou2023gmfpca,
     title = {Analysis of Active/Inactive Patterns in the NHANES Data using Generalized Multilevel Functional Principal Component Analysis},
     author = {Zhou, Xinkai and Wrobel, Julia and Crainiceanu, Ciprian M. and Leroux, Andrew},
     year = {2023},
     journal = {arXiv preprint arXiv:2311.14054},
   }

2022

1. Stat. Anal. Data Min.

   

   Bag of little bootstraps for massive and distributed longitudinal data

   Xinkai Zhou, Jin J Zhou, and Hua Zhou

   Statistical Analysis and Data Mining: The ASA Data Science Journal, 2022

   Abs Bib HTML Code

   Linear mixed models are widely used for analyzing longitudinal datasets, and the inference for variance component parameters relies on the bootstrap method. However, health systems and technology companies routinely generate massive longitudinal datasets that make the traditional bootstrap method infeasible. To solve this problem, we extend the highly scalable bag of little bootstraps method for independent data to longitudinal data and develop a highly efficient Julia package MixedModelsBLB.jl. Simulation experiments and real data analysis demonstrate the favorable statistical performance and computational advantages of our method compared to the traditional bootstrap method. For the statistical inference of variance components, it achieves 200 times speedup on the scale of 1 million subjects (20 million total observations), and is the only currently available tool that can handle more than 10 million subjects (200 million total observations) using desktop computers.

   @article{zhou2022blb,
     title = {Bag of little bootstraps for massive and distributed longitudinal data},
     author = {Zhou, Xinkai and Zhou, Jin J and Zhou, Hua},
     journal = {Statistical Analysis and Data Mining: The ASA Data Science Journal},
     volume = {15},
     number = {3},
     pages = {314--321},
     year = {2022},
     publisher = {Wiley Online Library},
   }